前言

正则表达式这个东西其实大家都或多或少接触过，给我的感觉就是:入门很简单，深入怕麻烦，写来一时爽，阅读很恶心。正好趁着学习分享的机会自己系统性的整理一下。

正文

简介&派别

大家平时能接触得到的正则，分为2大类别:类unix系统中使用的POSIX派，以及各种编程语言标准库中的PCRE派。后一个大家接触的较多一些。

POSIX
最早的时候正则可以说是五花八门，grep(Global Regular Expression Print)，egrep，awk，lex，sed等程序都支持正则，但是每个程序所支持的正则或多或少又和其他的有些不一样。于是在1986年，POSIX（Portable Operating System Interface）标准公诸于世，POSIX制定了不同的操作系统都需要遵守的一套规则，当然，正则表达式也包括其中。
PCRE
PCRE(Perl Compatible Regular Expressions)是一个Perl库，包括 perl 兼容的正则表达式库。1994年10月Perl 5发布，当时是www兴起的时候，而Perl语言是为了文本处理而发明的，所以Perl基本上成了web开发的首选语言。所以使用广泛的Perl被后来的其他语言所移植，这其中包括了Tcl, Python, .NET , Ruby, PHP, C/C++, Java等等。下文讲的正则表达式也是这个PCRE标准
更多关于正则派别介

正则表达式

首先准备好正则检查工具(我觉得正常人类阅读这个东西都会觉得很蛋疼)，接下来就开始一步步看看正则表达式

引

如果你在看一篇文章，你想搜索所有的 hi ，这时候你可以用正则表达式 hi。这就是一个最基本的正则表达式，他精确的匹配字符hi，如果开启了忽视大小写的选项的话，它可以匹配hi,HI,Hi,hI这四种情况中的任意一种。
然而，上面的表达式却有一个问题，他会匹配所有的 hi，比如 history，high 等等，他会把所有包含在其他单词中的hi全都找出来，这显然不是想要的效果。这时候使用:\bhi\b,可以达到想要的效果。
\b 是一个元字符。代表着单词的开头或结尾，也就是单词的分界处。他匹配一个位置:它的前一个字符和后一个字符不全是(一个是,一个不是或不存在)\w。
如果你要查询 hi xxxxx magic 这样的句式，而不在乎中间的xxx内容是什么，可以使用 \bhi\b.\bmagic\b**
在这里， . 是一个元字符，匹配:除了换行符以外的任意字符；而 **\ 同是元字符，不过它代表的不是字符，也不是位置，而是数量:它指定 * 前边的内容可以连续重复使用任意次以使整个表达式得到匹配。上面出表达式可以这样解释: 首先是单词hi，接下来是任意字符(非换行)，最后以magic单词结尾。
再看这个例子：0\d\d-\d\d\d\d\d\d\d\d 这个表达式匹配:0开头，紧跟2个数字，接下来是一个 “-“ ，后面再跟8个数字（其实就是电话号码）。这里的 \d 匹配：一位数字，而 - 他就是一个字符。
这个表达式这样写虽然没错，但是就很重复。这里就需要使用重复来避免，上述的表达式可以写成0\d{2}-\d{8}**，这里 **{2} 表示前面的 \d 必须连续重复匹配2次才行，**{8}** 同理。

元字符

上面一节中出现了一些元字符，所以应该也有了一些认知，以下是常用的一些元字符

元字符	说明
.	匹配除换行符外任何字符
\w	匹配字母，数字，下划线
\s	匹配任意的空白符
\d	匹配数字
\b	匹配单词的开始或结束
^	匹配字符串的开始
$	匹配字符串的结束

更多的例子：

\ba\w*\b
某个单词开始（\b），以a开头，接下来是任意数量的字母或数字(\w*)，最后结尾（\b）
\d+
匹配1个，或者更多连续的数字，在这里 + 和 * 是类似的功能，* 允许0-N次的重复,而 + 则是重复1-N次（至少需要有一次）
\b\w{6}\b
匹配6个字符的单词
^\d{5,12}$
这里用到了元字符 ^ 和 $**，他们都匹配一个位置，这一点和 **\b 有点类似，而 {5,12} 和前面的 {2} 类似，他表示需要重复5-12次，在这个区间外都不匹配，而因为使用了 ^ 和 $ 所以整个字符串都要用来和 \d{5,12} 来匹配，换句话说这个字符串必须是5-12的数字。（如果没有 ^ 和 $ 那么整个字符串会截取判断，比如一个17位的数字，会被判断为2个符合的数字前面12位以及后面 5位）
和忽略大小写类似，有的处理工具会有多行处理的选项，开启后 ^ 和 $ 的意义就变成了匹配行的开始处和结束处。

元字符的转义

有时候需要查找元字符本身，比如我就想查找一个 . 号 , 而 . 这个表达式代表的是除换行符外任何字符，这时候就得加上转义符 \，当然 \ 自己本身也要转义，得使用 \\ 来找到 \

重复

上面已经出现过很多匹配重复的方法了，比如 *, + , {2} , **{5,12}**，下面则列出所有用来表示重复的限定符

语法	说明
*	重复0或更多次
+	重复1或更多次
?	重复0或1次, 理解成是否存在也可以
{n}	重复n次
{n,}	重复n 或更多次
{n,m}	重复 n 至 m 次

几个重复的例子

^\w+
由于第一位 ^ 的限制，那么这个正则根据选择的情况，会匹配每行的第一个字符串或者全局的第一个字符串
0\d{2}-?\d{8}
匹配 021-12345678 或者 02112345678 这样的（电话）号码

字符类

字符类提供了只匹配一个特定集合的方法，可以看做是匹配型元字符的个性化定制。比如说，我想匹配所有的数字可以用 \d，匹配所有的字符可以用 . ，这些匹配元字符已经提供了。但如果我想要找到所有的元音，所有的偶数呢？这时候就可以用字符类来自己指定集合。

[aeiou]
字符集由方括号 [ ] 表示，括号内的每个字符都会匹配到，比如这个就是寻找所有元音字母的正则表达式
^\d*[24680]$
表示所有偶数：\d* 表示任意个数字，但最后一个数字必须是24680中的一个；同理那么奇数就是 ^\d*[13579]$
同时字符类也可以指定一个范围，比如这个 [0-9] 表达式，就和 \d 是一样的，他们都表示一位数字。同理 [a-z0-9A-Z_] 也等同于 \w（仅在英文字母情况下）

分支条件

分支条件用 | 来连接几个正则表达式，比如这样 表达式1|表达式2|… 。如同这个符号本身，这个就有点像或条件判断，满足表达式1 或表达式2 的都会被匹配到。

^\d*[123]$|^\d*[456]$|^\d*[7890]$
这个表达式虽然这么长，但是他表示的东西很简单和 ^\d*$ 一样表示任意数字，但是这里主要是解释分支。
该表达式由 | 分成3段，分别表示任何123结尾的数字，456结尾的数字，7890结尾的数字。3个条件由或连接，即为任意数字。
\d{3}-?\d{8}|\d{8}
这个表达式匹配可以带上区号的电话号码。这个号码可以匹配 12345678 或 021-12345678 或 02112345678，但是如果反过来写就会有些不同。
表达式 \d{8}|\d{3}-?\d{8} 与上一个区别在于是 a|b 和 b|a 的区别,但是这个无法匹配02112345678，这个和if中的判定有些类似，都是从左向右匹配，如果满足，那么后面的判定则不会执行。 02112345678 这个数字中前8位已经满足了 \d{8} ，所以后面的不会继续执行，这个需要注意。

分组

分组也很好理解，比如要重复单个字符，仅仅在字符后面加上重复符就好了，但是要重复多个字符呢？这时可以用小括号 () 来指定子表达式，也就是分组了。这样就可以对一个小组进行重复操作（当然也可以是其他操作）

下面是几个例子，可以比较一下区别：

a*
匹配任意个a字符 aaaaaaa
ab*
匹配a后紧跟任意个b的字符 abbbbbb
(ab)*
匹配任意个 ab组成的字符 abababababab
(a|b)*
匹配任意由a和b 组成的字符 aabbababaabaaaabb
(\d{1,3}.){3}\d{1,3}
这是一个简单的ip匹配，首先看小括号内的 \d{1,3}. 表示 1-3个数字加上点也就是，123. 这样的字符；括号后跟着 {3} 说明前面的子表达式得重复3遍，那就是 123.123.123. 这样，最后有跟上了1-3个数字，最终的效果就是 123.123.123.123
但是这个表达式是有bug的，他虽然能匹配格式，但是他会匹配到格式正确但不合法的ip地址（ipv4要求每一位0-255），比如 666.777.888.999。如果可以使用算术比较的话，可能会很简单的解决这个问题，但是很遗憾，正则表达式中不提供关于数学的任何功能，所以要实现这个功能就要用到分组，选择，字符类 来描述一个正确的ip地址：
((2[0-4]\d|25[0-5]|[01]?\d\d?).){3}(2[0-4]\d|25[0-5]|[01]?\d\d?)
这个表达式乍一看就很吓人，但是他和之前那个简单版本的其实类似，简单版本的核心部分是 \d{1,3}**，对应的这个表达式核心部分是 **(2[0-4]\d|25[0-5]|[01]?\d\d?) 这一子表达式。子表达式中用了分支条件分别是：
- 2[0-4]\d匹配 200~249
- 25[0-5] 匹配 250-255
- [01]?\d\d? 匹配 0-199
  接下来的理解就很容易了，不多说了。思考2个问题：这3个表达式的顺序是否可以变？这样写太麻烦了，可以下面这样写吗？

([0-255].){3}[0-255]

反义

取反操作也是在代码中很常见的操作，这个没什么多说的直接看下表

语法	说明
\W	匹配任意不是字母，数字，下划线的字符
\S	匹配任意不是空白符的字符
\D	匹配任意不是数字的字符
\B	匹配不是单词开头或者结束的位置
[^x]	匹配除了 x 以外的任意字符
[^aeiou]	匹配除了aeiou以外的任意字符

后向引用

在使用了小括号指定一个子表达式后，匹配这个字表达式的文本 就会被捕获，可以在表达式或者其他程序中做进一步的处理，默认情况下每个分组会自动从左向右（以分组的左括号为表示）有一个组号，第一个分组的组号是1，第二个是2…. 组号0代表整个正则表达式。
后向引用用于重复搜索前面某一个分组匹配的文本。用 \1 代替分组1捕获的文本，比如：

\b(\w+)\b\s+\1\b
整个表达式匹配重复的表达式，hello hello，ok ok 这样的字符。把他拆成 \b(\w+)\b 和 s+ 和 \1\b 这样分开理解可能会好一些，第一段表示任意一个单词，第二段表示至少有一个空格，第三段表示得和第一段捕获的那个单词一样
当然，也支持自己给分组命名，用了自动分组的话，分组一多表达式一长，那本身不方便的阅读就更吓人了。
可以使用 (?<命名>表达式) 或者 (?’命名’表达式) 来指定子表达式的组名。比如上一个 (\w+) 取名为 myWord可以这样写 (?<myWord>\w+) ;而需要使用这个捕获的内容，可以这样写 **\k<myWord>**。所以上面的例子用自命名的方式就会写成这样
\b(?<myWord>\w+)\b\s+\k<myWord>\b

小括号

这边得插一下，上面的的分组和后向引用都用到了小括号。在使用小括号的时候，有很多特定用途的语法，下面是一些常用的：详细的会在后文写

分类	语法	说明
捕获	(exp)	匹配exp,并捕获文本到自动命名的组里
	(?<name>exp)	匹配exp,并捕获文本到名称为name的组里，也可以写成(?’name’exp)
	(?:exp)	匹配exp,不捕获匹配的文本，也不给此分组分配组号
零宽断言	(?=exp)	匹配exp前面的位置
	(?<=exp)	匹配exp后面的位置
	(?!exp)	匹配后面不是exp的位置
	(?<!exp)	匹配前面不是exp的位置
注释	(?#comment)	这种类型的分组不对正则表达式的处理产生任何影响，用于提供注释让人阅读

零宽断言

这个理解起来可能会有些麻烦。首先他用于查找在某些内容之前或之后的位置（但是并不包含这些内容），比如说查找 某某说: 后面跟的内容，也就是说它好像 \b ^ $ 一样用来指定一个位置，这个位置应该满足一定的条件（即断言:用来声明一个应该为真的事实，正则表达式中只有当断言为真才会继续匹配），因此也被称作零宽断言

(?=exp)
零宽度正预测先行断言：它断言自身出现的位置的后面能够匹配表达式exp。这个解释还是有点抽象，看这个例子
1
"吃饭了吗"他笑着打了个招呼。
在这里我想知道 “他笑着打了个招呼” 的内容，可以这样写 [\u4e00-\u9fa5]+(?=”他笑着打了个招呼。) (这里的字符类表示汉字) 这里的零宽断言是 (?=”他笑着打了个招呼。) 用大白话来解释就是: 我每有一个满足 [\u4e00-\u9fa5]+ 的字符我就停下来看一看后面，紧跟的内容是不是和符合表达式 “他笑着打了个招呼。 （这里是全匹配）。如果后面的东西满足了断言表达式，那么这个位置前面的符合 [\u4e00-\u9fa5]+ 表达式的内容就会被找到，也就是 吃饭了吗

(?<=exp)
零宽度正回顾后发断言: 它断言自身出现的位置的前面能够匹配表达式exp。理解了上面那个 预测先行断言 那么理解这个 回顾后发断言 会方便一些。
1
我说:"吃了"
与上一个类似 (?<=我说:”)[\u4e00-\u9fa5]+ 这个表达式在断点处检查其前面是否可以匹配表达式 我说:” （这里是全等）如果匹配，则表示找到那个位置，然后从这个位置开始寻找后面满足表达式 [\u4e00-\u9fa5]+ 的内容，这就是我说的吃了。
(?<=<(\w+)>).*(?=</\1>)
这是一个同时使用了以上2种断言的例子，也用到了分组，后向引用。他匹配简单html标签(不含属性)内部的内容，如下例中的hello world!
1
<span>hello world!</span>
负向零宽断言

前面提到的取反是查找 不是某个字符或者不在某个字符类里 的字符的方法。但是如果只是想确保某个字符没有出现，而不去匹配它时呢？比如我想找： *a开头后面不是b的单词(匹配apple 不匹配abandon)*，我们也许可以这样写:

\ba[^b]\w*\b
这个匹配到所有a开头后面不是b的单词，但是他似乎也能匹配一些其他东西，比如： a piece of cake 中前半部分。因为 [^b] 总得匹配一个字符(会消费一个字符)，例子中 a 和 piece中的空格恰好匹配上了*[^b]。
这时候 **负向零宽断言就可以处理这个问题，因为他匹配一个位置，而不会消费字符。如果说把零宽断言理解成 if(true) ，那么这个负向零宽断言就是 if(false) 。那么现在可以这样来写这个需求：**\ba(?!b)\w\\b**
(?!exp)
这就是零宽度负预测先行断言: 断言一个位置的后面不能匹配表达式exp。比如 \b((?!ab)\w)+\b : 匹配不含 ab 的单词
(?<!exp)
同理，零宽度负回顾后发断言：断言一个位置的前面不能匹配表达式exp。比如 \b\w+(?<!ing)\b:匹配不是ing结尾的单词
ps:记住零宽断言找的是一个位置。

^(?=.*[a-z])(?=.*[A-Z])(?=.*\d)(?=.*\W)[^]{8,16}$ ps:这里的 [^] 等同于 [\s\S]
^(?![A-Z0-9\W]+$)(?![a-z0-9\W]+$)(?![A-Za-z\W]+$)(?![A-Za-z0-9]+$)[a-zA-Z0-9\W]{8,16}$
上面2个描述的都是输入密码的校验规则，密码长度8-16位，必须包含大小写字母，数字，特殊字符。上面的用的是零宽断言，下面用的是负向零宽断言。他们的关系就好像 if(result.isSuccess()) = if(!result.isFail()) 那样，用以判断的条件是相反的。但是看下来的“吓人”程度确实不一样的，平时使用的时候可以通过转化来使表达式稍微“可爱”一些。当然，前提是你确定写的2个条件是完全相反的，否则还是老老实实写自己有把握的那一个。（写相反条件有可能会漏掉一些情况）

注释

到现在看下来，上面出现的正则表达式还没有特别复杂的，但是阅读起来已经很麻烦了。所以正则表达式也提供了注释的写法。当然我自己不倾向于把注释直接写在表达式里面，感觉他会让这个表达式更恶心…但是学习还是要了解一下的：

(?#注释内容)
同样使用小括号作为注释的一部分…比如之前那个ip地址的正则表达式可以这样加上备注：
((2[0-4]\d(?#200-249)|25[0-5](?#250-255)|[01]?\d\d?(?#0-199)).){3}(2[0-4]\d|25[0-5]|[01]?\d\d?)
是不是感觉比原来阅读起来更麻烦了…这个就仁者见仁智者见智了。
ps:使用注释的时候，确保环境下支持注释。我自己目前没有尝试成功过…

贪婪与懒惰

正则在匹配有重复限定符(星号加号等等）的表达式时，通常的情况下，会在表达式满足的情况下，请可能匹配更多的字符。比如这个例子:

a.*b
这个正则匹配a开头，中间任意，以b结尾的的字符串。aabccba 这个字符串他会全部匹配，这就是贪婪匹配。
而有时候就需要懒惰匹配，也就是匹配尽可能少的字符。之前的那些重复限定符都可以加上 ? 来变成懒惰匹配模式。比如 .*? 就是匹配尽可能少的重复字符串。结合上面的例子：
a.*?b
启用了懒惰匹配后，现在就匹配 aabccba中的前三个字符。也许会有这个问题：为什么不只匹配第2-3个字符呢？ab不是更短么？因为正则表达式有另一条规则，比懒惰／贪婪规则的优先级更高：最先开始的匹配拥有最高的优先权——The match that begins earliest wins。

懒惰限定符：

语法	说明
*?	重复任意次，但尽可能少重复
+?	重复1或更多次，但尽可能少重复
??	重复0或1次，但尽可能少重复
{n,}?	重复n 或更多次，但尽可能少重复
{n,m}?	重复 n 至 m 次，但尽可能少重复

匹配模式

上面有提到过，匹配的时候可以选择忽视大小写，单行，多行这样的匹配模式。以java为例，Pattern 类也提供了几种处理方式，这边仅简单列出，详细的可以在 java.util.regex.Pattern 中查看

语法	说明
UNIX_LINES	启动Unix的行模式 ,在这个模式下，只有 \n 才被认作一行的中止，并且与 . ^ $ 进行匹配
CASE_INSENSITIVE	默认情况下，大小写不明感的匹配只适用于US-ASCII字符集。这个标志能让表达式忽略大小写进行匹配。要想对Unicode字符进行大小不明感的匹配，只要将UNICODE_CASE与这个标志合起来就行了。
COMMENTS	在这种模式下，匹配时会忽略(正则表达式里的)空格字符。注释从#开始，一直到这行结束。可以通过嵌入式的标志来启用Unix行模式。
MULTILINE	在这种模式下，’^’和’$’分别匹配一行的开始和结束。此外，’^’仍然匹配字符串的开始，’$’也匹配字符串的结束。默认情况下，这两个表达式仅仅匹配字符串的开始和结束。
LITERAL	启动字面量解析模式
DOTALL	在这种模式下，表达式’.’可以匹配任意字符，包括表示一行的结束符。默认情况下，表达式’.’不匹配行的结束符。
UNICODE_CASE	在这个模式下，如果你还启用了CASE_INSENSITIVE标志，那么它会对Unicode字符进行大小写不明感的匹配。默认情况下，大小写不敏感的匹配只适用于US-ASCII字符集。
CANON_EQ	当且仅当两个字符的”正规分解(canonical decomposition)”都完全相同的情况下，才认定匹配。比如用了这个标志之后，表达式”a\u030A”会匹配”?”。默认情况下，不考虑”规范相等性(canonical equivalence)”。
UNICODE_CHARACTER_CLASS	启用Predefined字符类和POSIX字符类的Unicode版本。

引擎

简介

上面一章主要写了一下正则表达式的语法，现在换个角度，正则是怎么工作的呢？
如果学习过编译原理的话，就会知道他的另一个名字 正规式，是一个表示正规集(正规式或正规文法表示的集合称为正规集)的工具。而提到正规集，总会联想到有穷自动机。有穷自动机作为一种识别装置，它可以准确的识别正规集，即识别正规文法所定义的语言和正规式所表示的集合。它又分为2类：NFA 和 DFA。在后文会简单展开一下。
上面说了一堆理论，有啥用呢？其实很多程序(语言)处理正则表达式的引擎就是上文提到的东西，粗见下表（很多程序大家应该都用过），详见正则表达式的几种引擎。

引擎	程序
DFA	awk (大多数版本)、egrep(大多数版本)、flex、lex、MySQL、Procmail
传统型NFA	GNU Emacs、Java、grep(大多数版本)、less、more、.NET语言、PCRE library、Perl、PHP(所有三套正则库)、Python、Ruby、sed(大多数版本)、vi
POSIX NFA	mawk、Mortice Kern Systems’ utilities、GNU Emacs (明确指定时使用)
DFA/NFA 混合	GNU awk、GNU grep/egrep、Tcl

上次写前缀树实现敏感词过滤的时候，用到了DFA。但是文章中没有展开详细写，再次遇到就趁这个机会写一下吧。

正规式

辅助字母表

设字母表为Σ，辅助字母表Σ’ = { Φ , ε , | , . , * , ( , ) }。
先解释一下这个辅助字母表

Φ 表示正规集 {} ，里面什么东西都没。
ε 表示正规集 {ε} , 里面只有一个一个元素：ε 。 ε表示空字符串。 ε和Φ的关系便于理解，不恰当的类比成 String a = null; 和 String b = “”;
| 表示或运算，也有地方是用 + 来表示的
. 表示连接，一般可以省略
* 表示闭包，即任意有限次的自重复连接。也就是上面讲的重复0或多次。
() 括号在优先级没有混淆的时候可以省略，优先级为 * > . > | (都是左结合的)

定义

下面是正规式和他表示的正规集的递归定义。

ε和Φ都是Σ上的正规式，他们表示的正规集分别为 {ε} 和 {}
任何a∈Σ，a是Σ上的一个正规式，他所表示的的正规集为{a}
假定e1和e2都是都是Σ上的正规式，他们所表示的正规集分别是L(e1) 和 L(e2)，那么(e1)，e1| e2，e1.e2，e1* 也都是正规式，他们所表示的正规集分别是，L(e1)，L(e1) | L(e2)，L(e1).L(e2)，(L(e1))*
仅有限次使用上面3步骤而定义的表达式才是Σ上的正规式，仅有这些正规式表示的字集才是Σ上的正规集。

一个例子：假设 Σ={a,b}，那么Σ上部分的正规式和其对应的子集有：

正规式	正规集
a	{a}
a\|b	{a,b}
ab	{ab}
(a\|b)(a\|b)	{aa,ab,bb,ba}
a*	{ε,a,aa,aaa,aaaa,…任意数量a的字符串}
(a\|b)*	{ε,a,b,aa,ab,ba,bb,….所有由字符a和b组成的字符串}
(a\|b)(aa\|bb)(a\|b)	Σ*上所有含有连续aa或bb 的字符串

代数规律

正规式的运算也满足一些代数规律，设r，s，t为正规式，那么：

r|s = s|r 或运算的交换律
r|(s|t) = (r|s)|t 或运算的结合律
(rs)t = r(st) 连接运算的结合律
r(s|t) = rs|rt 分配率
(s|t)r = sr|tr
εr = r ε是连接运算的恒等元素
rε = r
r|r = r 连接运算抽取律

DFA

全称为deterministic finite automaton，确定的有穷自动机。一个确定的有穷自动机M由5个部分组成：K，Σ，f，S，Z

K 是一个有穷集合，他的每一个元素称为一个状态
Σ是一个有穷字母表，他的每一个元素成为一个输入符号
f是转换函数，如果f(ki,a)=kj (ki∈K，kj∈K)。表示当前状态是 ki，输入字符为a时，将会转换到下一个状态kj。kj称为ki的一个后继状态。
S∈K，是一个唯一的初始状态
Z⊂K，是一个结束状态

现在来看一个简单例子，DFA M记作 = ({S,U,V,Q}，{a,b}，f，S，{Q})，其中f如下定义:

f(S,a)=U
f(S,b)=V
f(U,a)=Q
f(U,b)=V
f(V,a)=U
f(V,b)=Q
f(Q,a)=Q
f(Q,b)=Q

一个DFA可以表示成一个状态转换图，如果一个DFA N 含有m个状态，n个输入符号，那么这个状态图会有m个节点，每个节点最多有n和弧射出，整个图含有唯一的初始节点和若干个终节点。初始节点用=> 或者加以 - 表示，终节点用双圈或者加以 + 表示。如果f(ki,a)=kj，则从ki节点到kj节点画一条弧，弧上标记a。那么上面那个M 的状态图可以这样画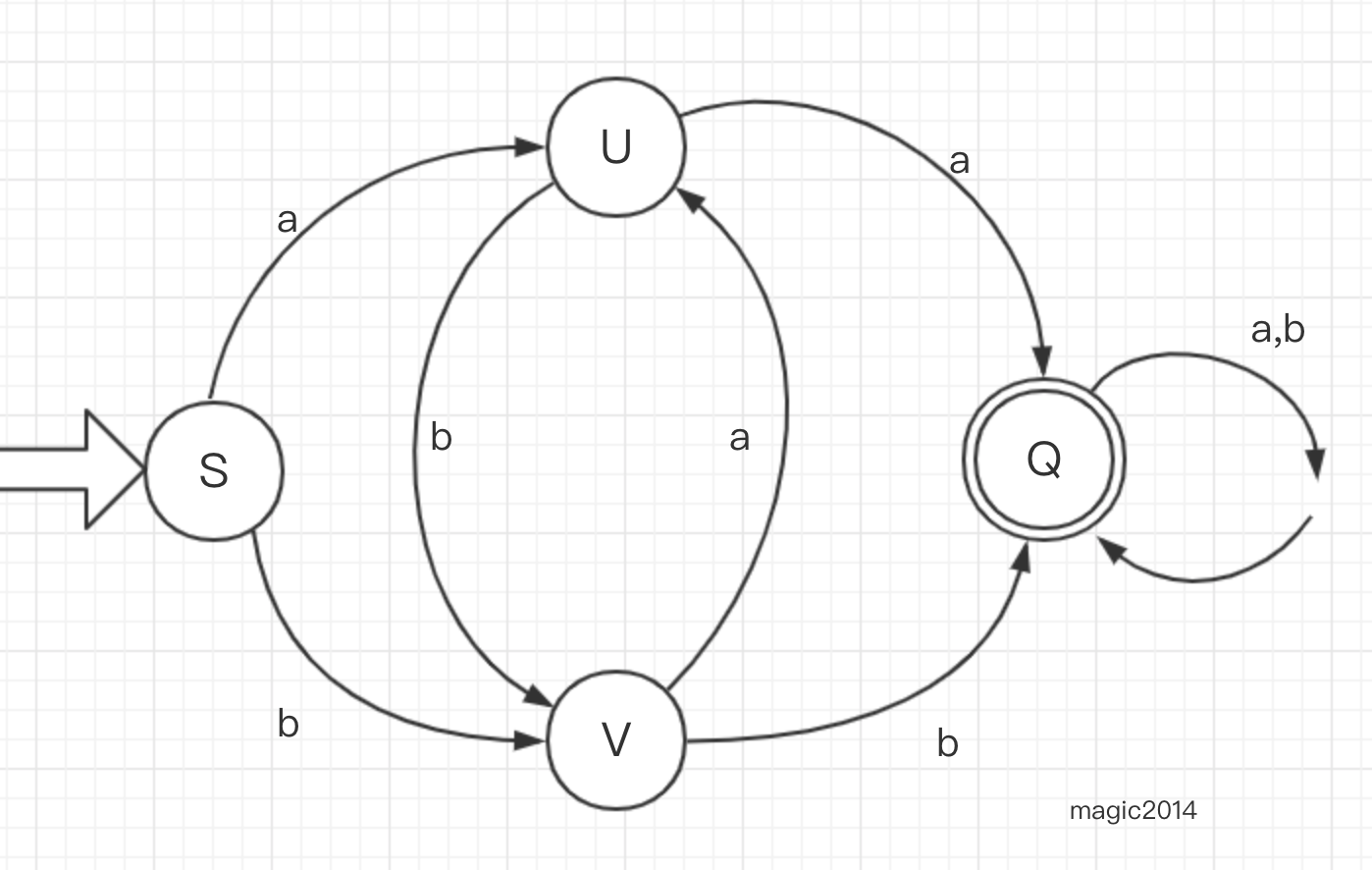

对于Σ*中的任何字符串t，如果存在一条从初始节点到某一终结点的路线，并且这条路线上所有弧的标记连接起来等于t，那么称t可以被DFA M 接受。如果初始节点同时也是终节点，那么空字符可以被M接受。

为了描述一个符号串t可以被DFA M接受，需要将上面的转换函数f扩充：

设C∈K，f(C,ε)=C 即表示如果输入的符号是空，就仍停留在原来的状态上
一个字符串t (String) 将他表示成 t1t2 的形式 (char) ，在DFA上的运行b定义为 f(C,t1t2) = f( f(C,t1) , t2 )
比如这样证明字符串 baab 可以被上面的 M 所接受：

f(S,baab) = f( f(S,b) , aab ) = f(V,aab) = f( f(V,a) , ab ) = f(U,ab) = f( f(U,a) , b ) = f(Q,b) = Q; 而Q是一个终结态，所以该字符串被M接受。
DFA的确定性表现在这个转换函数上，他是一个单值函数，也就是说，对于任何状态 k∈K，和输入符号 a∈Σ，f(k,a) 都唯一确定了下一个状态。从图上看，就是每一个节点所有向外画的弧中，不能有标记重复的弧。

NFA

全称为nondeterministic finite automaton，不确定的有穷自动机。同样的也由（K，Σ，f，S，Z）5个部分组成。其中 K Σ Z 和DFA定义相同。

S⊂K，是一个非空初状态集合
f是转换函数，与DFA类似，也是接受一个字符转换一个状态。不同的是，他不能确定去往哪一个后继状态。
依然看一个例子 NFA M 记作 ({0,1,2,3,4}，{a,b}，f，{0}，{2,4})，其中f如下定义：
f(0,a)={0,3}
f(0,b)={0,1}
f(1,b)={2}
f(2,a)={2}
f(2,b)={2}
f(3,a)={4}
f(4,a)={4}
f(4,b)={4}
状态图的画法与DFA类似: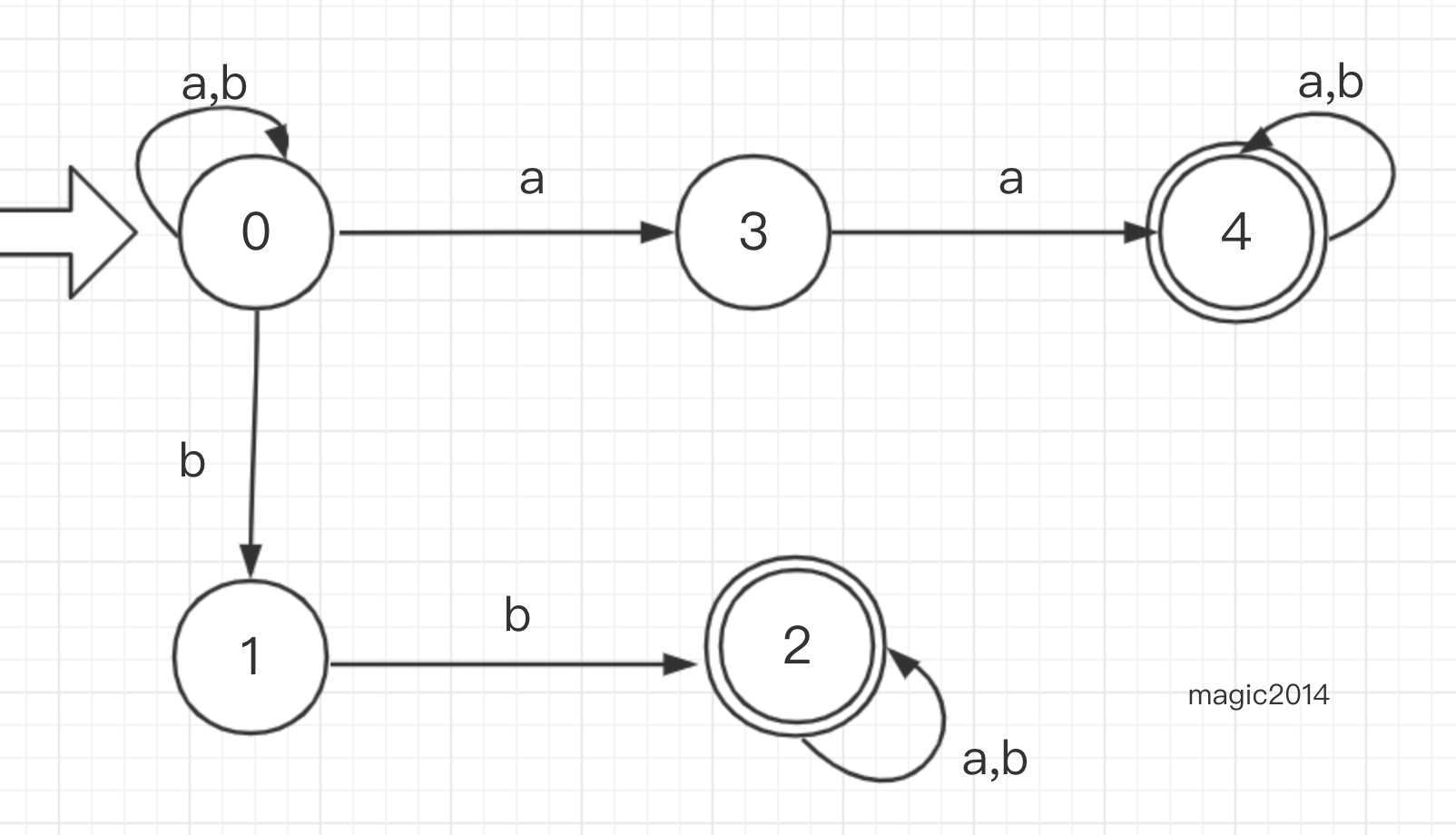

对于Σ*中的任何字符串t，如果存在一条从某一个初始节点到某一个终结点的道路，且道路上所有弧的标记字符连接成的串等于t，那么称t可以被NFA M 接受。其实看这里就可以察觉到了，DFA是NFA的一个特例。

NFA转化为等价DFA

DFA由于每一个状态的后继状态后确定，使得其效率更高（当然也有代价..）。有穷自动机有一个定理：设L为一个NFA接受的集合，则存在一个接受L的DFA。而常用的转换方法是子集构造法。
从上面的介绍NFA 和 DFA两节假设的转换函数可以看出，NFA的达到的状态一般是一个状态的集合，而在DFA中则是一个确定的状态。从NFA到DFA的基本想法是让DFA的每一个状态对应 NFA的一组状态。也就是让DFA使用它的状态，去记录在NFA接收一个字符后可能达到的所有状态，在接收字符串a1a2a3…an 之后，DFA处于这样一个状态：该状态表示这个NFA的一个子集T，T是从NFA的开始状态，沿着a1a2a3…an可以到达的那些状态构成的。
ps:子集构造法的过程展开写一下东西还挺多的（先挖坑，有空再填）。请看下集

正则表达式转换有穷自动机

其实节的小标题不太恰当，应该是 正规式和有穷自动机的等价性。因为在编译原理中 正规式 和 有穷自动机是可以互相转化的，但是由M 转化为r 在本文中关系不大，而且篇幅..也挺大的..所以仅写一下看这篇文章的人可能会关注的问题，也就是： 正则表达式转换为有穷自动机
在编译原理中，从Σ上一个正规式r，构造Σ上的一个等价的 NFA M 的方法称为 语法制导 。即按照正规式的语法结构指引构造过程，首先将正规式分解成一系列的子表达式，然后使用下面的规则构造NFA。

字符转化

对于正规式Φ ，构造的NFA为:
对于正规式ε，构造的NFA为：
对于正规式 a，a∈Z，所构造的NFA：

运算符转化

若s，t为Σ上的正规式，相应的NFA分别记作 N(s) 和 N(t)则

对正规式 r = s|t ，所构造的NFA(r)为：

其中x是NFA(r)的初始状态，y是终结状态，x到N(s)和N(t)的初始状态各有一个ε弧；同样的，从N(s)和N(t)的终结状态各有一个ε弧到y。现在N(s)和N(t)的初始状态和终结状态已经不作为N(r)的初始和终结态了。（有点抽象的意思）
对正规式 r=st，构造的NFA(r)为：

其中N(s)的初始态成为了N(r)的初始态，N(t)的终结态成为了N(r)的终结态。而N(s)的终结态和N(t)的初始状态合并为N(r)的一个中间状态 (头尾相接)
对于正规式r=s*，构造的NFA(r)为：

这是的x和y分别是N(r)的初始和终结状态，从x引ε弧到N(s)的初始态，从N(s)的终结态引ε弧到y；从x到y引ε弧；从N(s)的终结态ε弧到N(s)的初始态(这2个状态称为N(r)的中间状态)。
正规式(s) 和 s 的NFA 一样。（括号只是改变运算优先级，本身不参与运算）

举个栗子

下面直接来看一个简单的栗子，将上面提到的转化方式全部都用一下

为 r = (a|b)*abb 构造NFA N

从左往右分解r，令r1 = a。根据上面的字符转化第三条，很容易就画出来
然后遇到运算符 | 先跳过，遇到了字符 b，令r2 = b。转化同上
然后令将 a|b 连起来看。令 r3 = r1|r2 。根据运算符转化第1条，如下转化
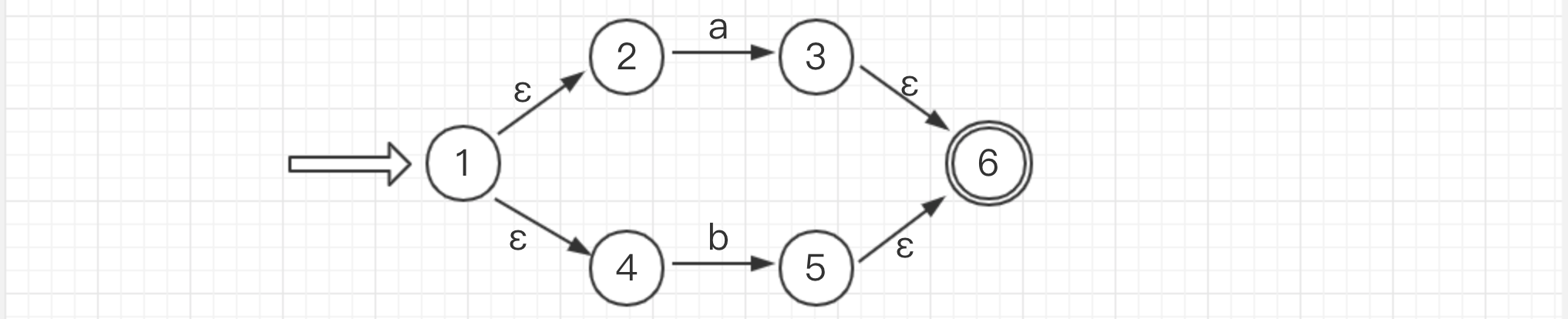
接着读取下一个运算符 * 。令 r4 = r3*。运算符转化第三条（这边其实跳过了括号的转化，因为他仅表现一个优先级）
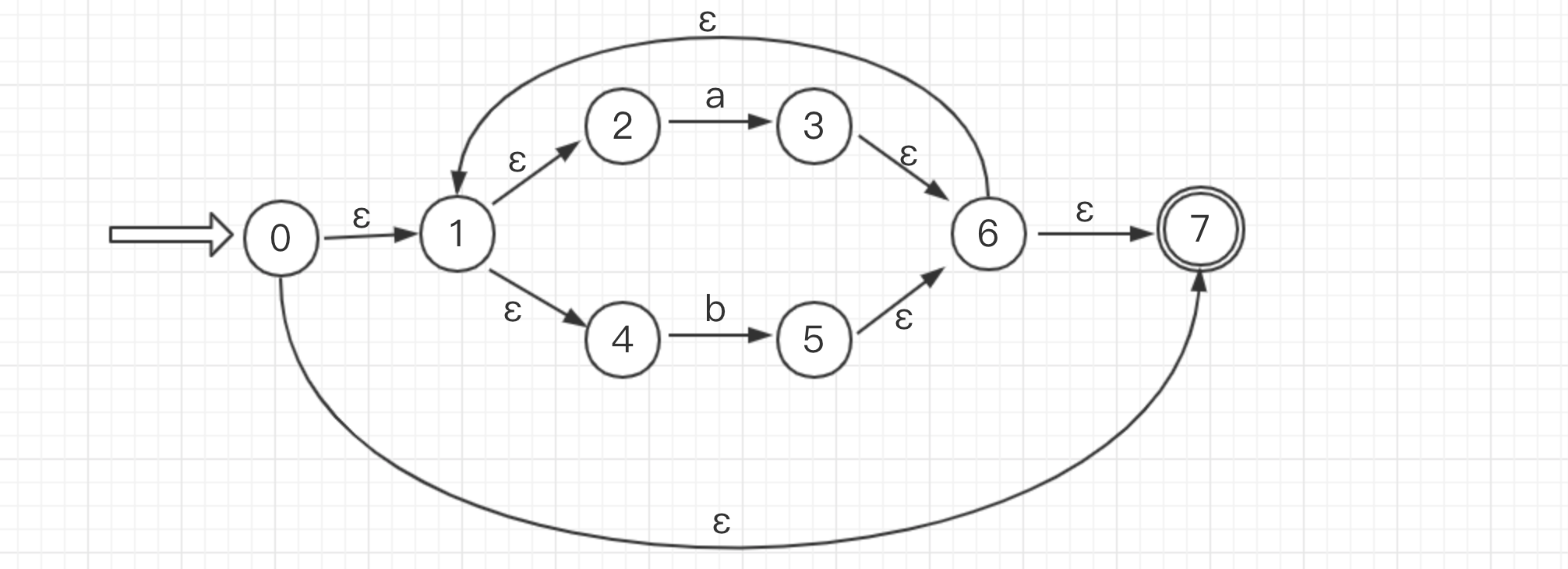
接下来读取到字符 a b b，由于他们都是连接运算，所以比较简单（字符转化第二条）。令 r5 = a。 r6 = b。 r7=b。则有 r8 = r5r6。r9=r8r7。最后将前半部分和后半部分连接，r10 = r4r9。(这一步图比较简单，所以一步到位画完了)

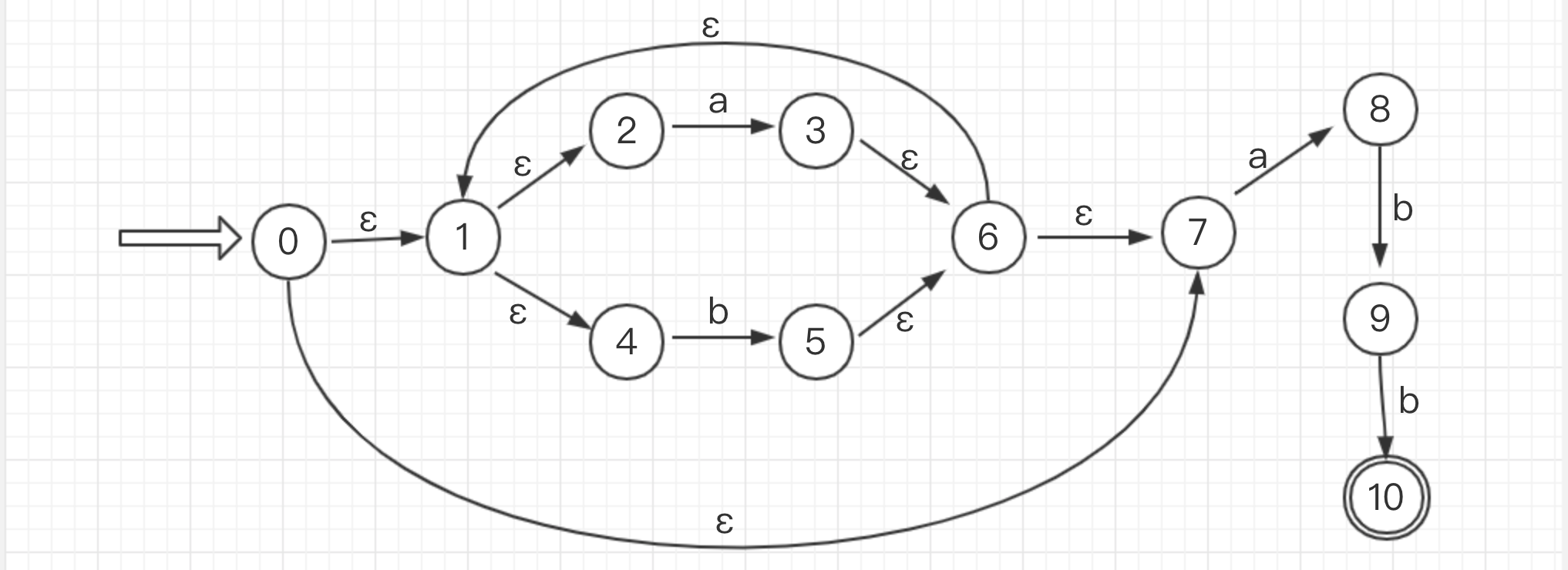
当然除了这样从左往右分解分解r，还有很多方法分解：

令 r1 = (a|b)* , r2 = abb 则有 r3 = r1r2
令 r4 = a|b ，则可以令 r1 = r4* 。字符转化第三条将 * 转化
这一步简单来说，直接将 a|b 拆成2条弧即可
接下来对于r2(abb)的处理同上，转化后连接在前半部分即可

对于第三步得补充一下，如果要严格根据转化方法的话，应该要令r5=a，r6=b，r4=r5|r6，这样一系列操作，最后转化的样子应该是上一种方式第3步出来的东西。乍一看这两种图看起来不太一样，但是他们确实表示的是同一个r，由于第一种方式转化出了很多 ε弧，而ε在连接运算时是一个恒等符。不恰当的例子数学上 2+3 = 5 可以写成 2x1x1x1 + 3x1x1x1 = 5 ，但是没人会怎么写，后者可以化简为前者。同样的有穷自动机也是可以通过消除多余状态来化简的，这一般被用于DFA中。化简的部分与本文关系不大就不多写了…

简单实现DFA

在这边我自己用java简单实现了一下DFA，下面直接贴代码:

import java.util.List;
import java.util.Map;
import java.util.stream.Collectors;

/**
 * 
 * @ClassName: DFA
 * @Description: java实现一下DFA K，Σ，f，S，Z
 * 
 *               K 是一个有穷集合，他的每一个元素称为一个状态 状态集合 
 *               Σ是一个有穷字母表，他的每一个元素成为一个输入符号 字符集
 *               f是转换函数，如果f(ki,a)=kj (ki∈K，kj∈K)。表示当前状态是 ki，输入字符为a时，将会转换到下一个状态kj。kj称为ki的一个后继状态。 
 *               S∈K，是一个唯一的初始状态
 *               Z⊂K，是一个结束状态
 * 
 * @author: chenhaoyu
 * @date: Dec 6, 2019 6:07:35 PM
 */
public class DFA {
    List<String> K;
    List<Character> Σ;
    Map<String, List<Func>> funcs;
    String S;
    List<String> Z;
    /**
     * 
     * @param K 一个有穷集合，他的每一个元素称为一个状态 状态集合 
     * @param Σ 一个有穷字母表，他的每一个元素成为一个输入符号 字符集
     * @param funcs 转换函数，如果f(ki,a)=kj (ki∈K，kj∈K)。表示当前状态是 ki，输入字符为a时，将会转换到下一个状态kj。kj称为ki的一个后继状态。 
     * @param S∈K，是一个唯一的初始状态
     * @param Z⊂K，是一个结束状态
     */
    public DFA(List<String> K, List<Character> Σ, List<Func> funcs, String S, List<String> Z) {
        this.K = K;
        this.Σ = Σ;
        this.funcs = funcs.stream().collect(Collectors.groupingBy(Func::getKi));
        this.S = S;
        this.Z = Z;
    }
    /**
     * 
     * @Description:检查字符串是否被该DFA接受
     * @param str
     * @return
     * @author: chenhaoyu
     * @time:Dec 10, 2019 11:05:19 AM
     */
    public boolean checkString(String str) {
        return check(str.toCharArray(),0,S);
    }
    
    /**
     * 
     * @Description:内部递归实现
     * @param chArray
     * @param index
     * @param state
     * @return
     * @author: chenhaoyu
     * @time:Dec 10, 2019 11:17:41 AM
     */
    private boolean check(char[] chArray , int index , String state) {
        char ch = chArray[index];
        // System.out.println(ch); // 打印当前char
        if (Σ != null && !Σ.contains(ch)) {
            System.out.println("非法字符 '"+ch+"' 不包含在指定的 Σ 字母表中");
            return false;
        }
        Map<Character,String> f = funcs.get(state).stream().collect(Collectors.toMap(Func::getCh,Func::getKj));
        String nextState = f.get(ch);
        if (index == chArray.length-1) {
            if (Z.contains(nextState)) {
                return true;
            }else {
                System.out.println("该字符串\""+new String(chArray)+"\"不被 此DFA接受");
                return false;
            }
        }else {
            index ++;
            return check(chArray, index, nextState);
        }
    }
}



/**
 * 
 * @ClassName: func
 * @Description: 转换函数bean f(ki,ch)=kj (ki∈K，kj∈K)
 * @author: chenhaoyu
 * @date: Dec 6, 2019 6:23:48 PM
 */
class Func {
    // 当前状态
    private String ki;
    // 接受字符
    private char ch;
    // 后继状态
    private String kj;

    public Func(String ki, char ch, String kj) {
        this.ki = ki;
        this.ch = ch;
        this.kj = kj;
    }

    public char getCh() {
        return ch;
    }

    public String getKi() {
        return ki;
    }

    public String getKj() {
        return kj;
    }
}

试运行一下，在这里就构造DFA那一节中的那个M 为例:

@Test
public void testdfa() {
    //构造转换函数
    List<Func> funcs = new ArrayList<>();
    funcs.add(new Func("S", 'a', "U"));
    funcs.add(new Func("S", 'b', "V"));
    funcs.add(new Func("U", 'a', "Q"));
    funcs.add(new Func("U", 'b', "V"));
    funcs.add(new Func("V", 'a', "U"));
    funcs.add(new Func("V", 'b', "Q"));
    funcs.add(new Func("Q", 'a', "Q"));
    funcs.add(new Func("Q", 'b', "Q"));
    //构造dfa
    DFA dfa = new DFA(Arrays.asList("S","U","V","Q"), Arrays.asList('a','b'), funcs, "S", Arrays.asList("Q"));
    
    //测试1
    System.out.println(dfa.checkString("abab"));
    // console 输出:
    // 该字符串"abab"不被 此DFA接受
    // false
    
    //测试2
    System.out.println(dfa.checkString("ababc"));
    // console 输出:
    // 非法字符 'c' 不包含在指定的 Σ 字母表中
    // false
    
    //测试3
    System.out.println(dfa.checkString("abbba"));
    // console 输出:
    // true
    
}

由于用的java，于是直接将转换函数构造成了一个对象模型，这样便于阅读和理解。同时DFA也根据其概念描述来构造(当然怎么设计DFA的实现还有很多其他方法)，总之阅读上应该没有什么问题。内部方法check用了递归实现，一是效率更高一些，二是写起来比较方便。但是这可能会有潜在的问题：当遇到一个超级长的str的时候，内存可能占用过大。当然一般情况也不会遇到这个问题，真的要解决的话就将递归实现改为循环实现就好了。

结语

总算找了个时间学习了一下正则，同时复习了一下编译原理倒是让我挺意外的。由于使用语言的差别，java有一些正则的语法不支持比如说平衡组。而且我在测试写的内容的时候，发现很多正则测试工具也不能支持。综合考虑就省略了一些正则方面的高级操作。仅写了一些基本常用操作。作为补偿，后面加了关于正则引擎的简单介绍。
这次就到这里，感谢阅读。

参考资料

上文参考了以下内容，感谢原作者的精彩文章。

前言

正文